Omgaan met (sociale) media.
Studenten hebben eerder les gehad over nepnieuws, desinformatie en/of misinformatie. Deze les is een vervolg en geeft studenten houvast in een zoektocht naar betrouwbare informatie.
Open de les met een stukje herhaling over de begrippen nepnieuws, desinformatie en misinformatie. Wat is het en waarom zijn deze begrippen belangrijk? Je kunt de uitleg ondersteunen met materiaal van de NOS, bijvoorbeeld deze video of dit artikel.
We zijn dol op cijfers. Lijstjes, beoordelingen en rangordes geven overzicht, maar in hoeverre is het handig om je leven te laten leiden door cijfers? Klopt het wel altijd? In deze les staan jullie stil bij de manier waarop cijfers worden verzameld en hoe je hier het beste mee om kan gaan.
Voorbeeld 1
In 2017 kwam het nieuwsbericht naar buiten dat er een ware leegloop was ontstaan in de provincie Zeeland. Inwoners vertrokken naar de Randstad of naar grotere steden in de provincie zelf. Het platteland was niet meer in trek. De media bericht er over en verschillende bronnen laten weten dat er ernstige gevolgen aan kunnen hangen. Bij de leegloop van gemeenten kan het zijn dat scholen moeten sluiten of dat een huisartsenpost verdwijnt. De informatie kwam uit een rapport dat is opgesteld voor het Planbureau en bibliotheek van Zeeland. Een grafiek uit dit rapport laat de leegloop zien:
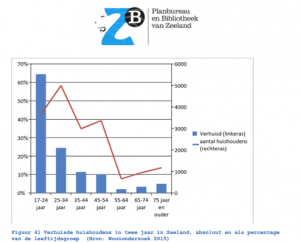
Dit rapport was weer gebaseerd op een indeling die door het CBS wordt gebruikt. Die indeling laat weten wanneer een gemeente doorgaat als een dorp of een stad. De definitie die het CBS hanteert is in 2015 gewijzigd. De leegloop die te zien is in de grafiek is daarom niet feitelijk aanwezig, maar alleen op papier doordat de grens over wanneer een gemeente wordt gezien als platteland of als een stad is gewijzigd.
Dit voorbeeld laat zien dat je moet nadenken over wat cijfers werkelijk zeggen en waar cijfers voor worden ingezet. Cijfers lijken steeds belangrijker te worden. Zo gebruiken verzekeraars cijfers om te berekenen hoeveel premie je moet betalen of gebruikt de Belastingdienst cijfers om in te schatten wie in de samenleving in de toekomst wellicht fraude kan plegen.
Het belang van cijfers is toegenomen na invoering van het Internationale Stelsel van Eenheden in 1960. Het is namelijk makkelijker praten wanneer iedereen dezelfde maten aanhoudt. Dit wanneer het over afstand gaat, dat iedereen dan praat over kilometers en niet iemand over mijlen en de ander over een yard of inches.
Vraag aan de klas: het verzamelen en verwerken van cijfers wordt statistiek genoemd, waar is het woord statistiek van afgeleid? Antwoord: staat
Vraag aan de klas: waarom is het afgeleid van het woord staat? Antwoord: Het is vaak vanuit de staat dat de vraag voor cijferverzameling ontstaat en ook door de staat wordt georganiseerd.
Tip: Deze video van één van onze docenten kan verder helpen bij het begrijpen van datavisualisatie.
Niet alles is vastgelegd in het internationale stelsel en ook niet iedereen is aangesloten. Zo wijkt Amerika af door gebruik te maken van mijlen en niet van kilometers. De telling van de minuten, uren, dagen en maanden is ook niet vastgelegd. Er bestaan verschillende kalenders. Het is niet voor iedereen hetzelfde jaar.
Vraag aan de klas: zoek een land of cultuur die een andere kalender heeft. Voorbeelden: Japan, Thailand islamitische kalender, Hebreeuwse kalender.
Soms zorgt een onderzoek voor een schokkende uitkomst. Zo zijn er meerdere wetenschappelijke onderzoeken die aantonen dat het gemiddelde IQ van zwarte mensen lager is dan van witte mensen. Zo bijvoorbeeld ook het onderzoek van Dickens en Flynn uit 2006 of onderzoek uit 2010 van Steven Carr.
Bekijk de grafiek via Padlet en vraag aan de studenten welke kritische vragen ze moeten stellen bij het zien van de grafiek. Voorbeelden:
- Hoeveel mensen deden mee?
- Waren de groepen even groot?
- Uit welke regio kwamen de deelnemers?
- Hoe zijn ze geselecteerd?
- Hoe is het IQ gemeten?
- Wat is zwart en wit eigenlijk?
Een gemiddelde zegt niet altijd wat over een groep. In een groep mensen zullen er altijd slimme mensen zijn en wat minder slimme mensen. Een gemiddelde staat dan eigenlijk voor niemand. Dat een gemiddelde niet altijd wat zegt, blijkt ook het volgende voorbeeld:
In een bus zitten vier passagiers. Één is advocaat en verdient €6400 per maand. Iemand anders werkt in de reclame en verdient €3500 euro, de derde persoon kookt eten in een verzorgingstehuis voor €1900 per maand en de vierde heeft zijn eigen marketingbedrijf dat haar maandelijks €2500 oplevert. Wat is het gemiddelde salaris? Antwoord: €3575.
Nu loopt Bill Gates de bus in, wat is het gemiddelde salaris nu? Antwoord: het vermogen van Bill Gates is 111 miljard euro. Wanneer hij de bus inloopt is iedereen opeens miljonair. Soms moet je niet kijken naar een gemiddelde maar naar het modale: meest voortkomende.
Tip: Wil je met je studenten verder in gesprek over het thema ‘kritisch denken’? Dan kun je deze praktische handleiding van Paul Hartog bespreken.
In de media worden er regelmatig ranglijsten gepubliceerd: de lekkerste oliebollen volgens het AD, het beste ziekenhuis volgens Elsevier of de leukste winkelstraat van Nederland volgens de Libelle. Het zijn overzichten waar veel Nederlanders hun keuze op baseren, maar is de volgorde wel altijd terecht?
Geef studenten onderstaande opdracht.
Zoek een ranglijst die gepubliceerd is en geef vervolgens antwoord op de volgende vragen:
- Waar is het gepubliceerd?
- Wat zegt de bron voor jou over het onderzoek?
- Hoe is het onderzoek uitgevoerd? (hoeveel mensen deden er mee, hoe zijn de vragen gesteld)
- Kan je de cijfers ook op de andere manier uitleggen?
- Kan je een bron vinden die deze cijfers tegenspreekt?
Opdracht vereenvoudigd
Kijk samen naar de oliebollentest van het AD en hoe de hoofdredacteur van de krant in talkshow Jinek moest toegeven dat er was geknoeid met de uitslag. Bespreek met de studenten wat ze hiervan vinden.
Verdiepingsopdracht
Zoek een ranglijst die gepubliceerd is en formuleer kritische vragen die je kunt stellen bij het zien van de cijfers. Wat heb je geleerd van de voorbeelden in de les en hoe kan je die kennis toepassen op jouw eigen voorbeeld? Formuleer vijf kritische vragen en geef er dan zelf antwoord op.
Studenten koppelen terug welke informatie ze hebben gevonden en hoe zij voortaan kijken naar cijfers.



 Dit is een product van het Practoraat Mediawijsheid. Onze lessen vallen onder de
Dit is een product van het Practoraat Mediawijsheid. Onze lessen vallen onder de 